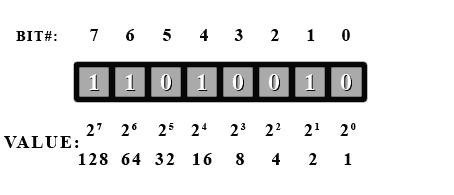Ah a little down one of the side paths of amateur radio for this question from the General Class exam pool.
How many states does a 3-bit binary counter have?
A. 3
B. 6
C. 8
D. 16
The answer depends on us knowing how to count in binary. Essentially the question is asking us what the maximum number of an 3-bit integer is. Your first instinct is probably to yell out “well 3 of course!”
But you’d be wrong. Let’s look at why.
In a 3-bit counter, there are (wait for it) three places that can either be a 1 or a 0.
So, for example. 010, or 100, or 111, or 001… It should start to make sense.
Here’s the pro-tip of the day. The maximum number of states in a binary system depends solely on the number of bits, and the answer is always 2^{n} where n is the number of bits.
So, ergo qed and all that nonsense, the answer is 2^{3}. Or 8. 1*2 is 2, 2*2 is 4, and 4*2 is 8.
The answer is C) 8.
Now I know what you’re thinking. “What does this have to do with amateur radio?” And on the surface its a valid question. But when you start getting into digital modes and encodings, bit rates and how much information can be sent in a given time period with a given signal type… This starts to matter.
Strictly speaking, though, its not likely to come up in day-to-day amateur radio operations. They just want you to be prepared.
Here’s the table of all the possible states of a 3-bit integer:
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
[G7B05]